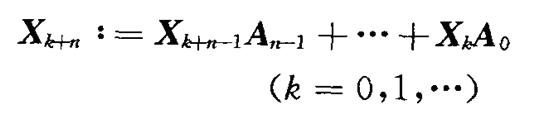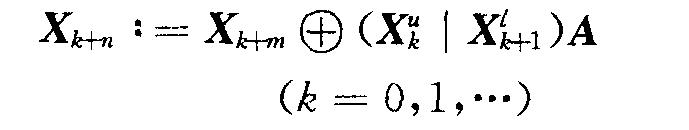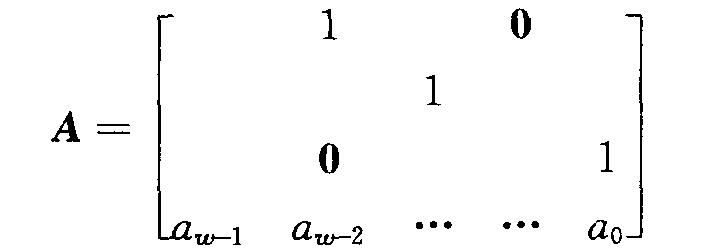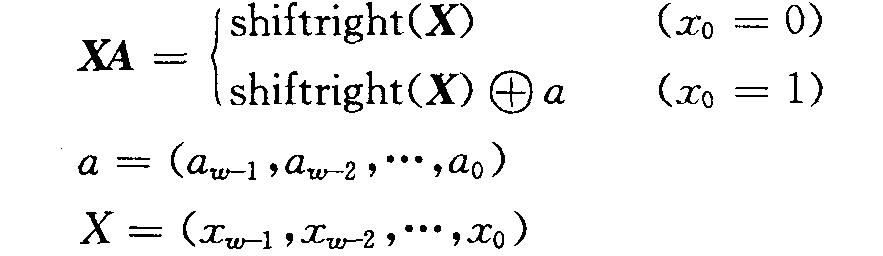亂數產生器-Mersenne Twister Random Number Generator
出自KMU Wiki
| 在2008年5月2日 (五) 01:57所做的修訂版本 (編輯) Mo (對話 | 貢獻) ←上一個 |
當前修訂版本 (2008年5月2日 (五) 02:43) (編輯) (撤銷) Mo (對話 | 貢獻) |
||
| 第1行: | 第1行: | ||
| - | Mersenne Twister(簡稱MT | + | ''''''Mersenne Twister(簡稱MT'''''''''): |
| + | <br> | ||
| - | + | <br>在1998年由Makoto和Takuji提出的,是多重遞迴矩陣方法(MRMM)中的一種,MRMM是在F<sub>2</sub>域上由線性遞推式: | |
| [[Image:MRMM.JPG]] | [[Image:MRMM.JPG]] | ||
| - | <br> | + | <br>產生隨機向量序列。X<sub>k</sub>是列向量,Ai是Wx W矩陣。 |
| - | 而MT演算法產生一個字(word)向量序列,看作是[0, | + | 而MT演算法產生一個字(word)向量序列,看作是[0,2<sup>w</sup>-1]間的均勻隨機整數。除以2<sup>w</sup>-1,認為每個字向量為[0,1]的一個實數。 算法如下: |
| [[Image:MRMM-1.JPG]] | [[Image:MRMM-1.JPG]] | ||
| + | <br> n=遞推式的維數,0<=r(隱藏於X上標u下標k的定義中)<=w-1,1<=m<=n 。給出X<sub>0</sub>,X<sub>1</sub>,...X <sub>n-1</sub>作為初始點,那麼X<sub>n</sub>由上面的式子再k=0時產生,令k=1,2,...,亂數產生器逐步產生X<sub>n+1</sub>,X<sub>n+2</sub>,...,在式子的右邊,Xuk意味著X<sub>k</sub>前w-r位,因此如果X=(X<sub>w-1</sub>,X<sub>w-2</sub>,...,X<sub>0</sub>),那麼由定義,X<sub>u</sub>是w-r維向量(X<sub>w-1</sub>,...,X<sub>r</sub>),X<sub>t</sub>是r維向量(X<sub>r-1</sub>,...,X<sub>0</sub><sub></sub>)。因此(X上標u下標k | X上標t下標k+1)恰好是一個並列,即X<sub>k</sub>前w-r位和X<sub>k+1</sub>的後r位按順序並列再一起得到的一個向量。矩陣A乘在這個向量的右邊。(XOR舉例:1 XOR 1=0 XOR 0,1 XOR 0=0 XOR 1=1) | ||
| - | + | <br> | |
| + | <br>對於上式,如果r=0,它變為X<sub>k+n</sub><sub></sub> = X<sub>k+n</sub> XOR X<sub>k</sub><sub></sub>A,即變成Matsumoto和Kurita提出的TGFSR。如果r=0且A=I,它又變為X<sub>k+n</sub> = X<sub>k+m</sub> XOR X<sub>k</sub>,即Lewis和Payne提出的GFSR。 | ||
| - | & | + | 為了使乘A計算速度較快,選擇 |
| + | |||
| + | [[Image:MRMM-2.JPG]] | ||
| + | |||
| + | 那麼計算XA可僅僅使用位運算: | ||
| + | |||
| + | [[Image:MRMM-3.JPG]] | ||
| + | |||
| + | <br> MT有以下優點:隨機性好,在計算機上容易實現,佔用記憶體較少(mt19937的C程式碼執行僅需624個字的工作區),與其它已使用的亂數產生器相比,產生隨機數的速度快、週期長,可達到2<sup>19937</sup>-1,且具有623維均勻分布的性質。 | ||
| + | |||
| + | <br> 雖然MT在許多方面較其他產生器優越,但它還是有一些缺點,即它所產生的序列是 | ||
| + | |||
| + | <br>高維均勻性的,還不夠完善。 | ||
當前修訂版本
'Mersenne Twister(簡稱MT''''):
在1998年由Makoto和Takuji提出的,是多重遞迴矩陣方法(MRMM)中的一種,MRMM是在F2域上由線性遞推式:
產生隨機向量序列。Xk是列向量,Ai是Wx W矩陣。
而MT演算法產生一個字(word)向量序列,看作是[0,2w-1]間的均勻隨機整數。除以2w-1,認為每個字向量為[0,1]的一個實數。 算法如下:
n=遞推式的維數,0<=r(隱藏於X上標u下標k的定義中)<=w-1,1<=m<=n 。給出X0,X1,...X n-1作為初始點,那麼Xn由上面的式子再k=0時產生,令k=1,2,...,亂數產生器逐步產生Xn+1,Xn+2,...,在式子的右邊,Xuk意味著Xk前w-r位,因此如果X=(Xw-1,Xw-2,...,X0),那麼由定義,Xu是w-r維向量(Xw-1,...,Xr),Xt是r維向量(Xr-1,...,X0)。因此(X上標u下標k | X上標t下標k+1)恰好是一個並列,即Xk前w-r位和Xk+1的後r位按順序並列再一起得到的一個向量。矩陣A乘在這個向量的右邊。(XOR舉例:1 XOR 1=0 XOR 0,1 XOR 0=0 XOR 1=1)
對於上式,如果r=0,它變為Xk+n = Xk+n XOR XkA,即變成Matsumoto和Kurita提出的TGFSR。如果r=0且A=I,它又變為Xk+n = Xk+m XOR Xk,即Lewis和Payne提出的GFSR。
為了使乘A計算速度較快,選擇
那麼計算XA可僅僅使用位運算:
MT有以下優點:隨機性好,在計算機上容易實現,佔用記憶體較少(mt19937的C程式碼執行僅需624個字的工作區),與其它已使用的亂數產生器相比,產生隨機數的速度快、週期長,可達到219937-1,且具有623維均勻分布的性質。
雖然MT在許多方面較其他產生器優越,但它還是有一些缺點,即它所產生的序列是
高維均勻性的,還不夠完善。