心理實驗法extra講:為什麼要考改錯題
出自KMU Wiki
(修訂版本間差異)
| 在2007年12月30日 (日) 12:14所做的修訂版本 (編輯) Sakurai (對話 | 貢獻) (新頁面: = Psychologist, how to = <br> === 國中為何學數學? === * 買菜有用嗎? ** 國小四則運算即可 * 統計用得到嗎? ** 一點點(如開根號) ** 其實計算...) ←上一個 |
當前修訂版本 (2014年11月21日 (五) 22:48) (編輯) (撤銷) Hyolics (對話 | 貢獻) (→心實為何考改錯?<br>) |
||
| (6個中途的修訂版本沒有顯示。) | |||
| 第5行: | 第5行: | ||
| === 國中為何學數學? === | === 國中為何學數學? === | ||
| - | * 買菜有用嗎? | + | * 買菜有用嗎? |
| ** 國小四則運算即可 | ** 國小四則運算即可 | ||
| - | * 統計用得到嗎? | + | * 統計用得到嗎? |
| ** 一點點(如開根號) | ** 一點點(如開根號) | ||
| ** 其實計算上會用計算機就好了 | ** 其實計算上會用計算機就好了 | ||
| 第24行: | 第24行: | ||
| * 即證明三角形ABD與三角形BAC全等(還有其他證法) | * 即證明三角形ABD與三角形BAC全等(還有其他證法) | ||
| - | <br> | + | 因為 |
| + | |||
| + | 線段AD=線段BC | ||
| + | |||
| + | 角ADC=角BCD | ||
| + | |||
| + | [[Image:Recten.png|thumb|right|試證矩形對角線等長]]線段DC=線段CD<br> | ||
| + | |||
| + | 故三角形ADC全等 三角形BCD(SAS) | ||
| + | |||
| + | 推得線段AC=線段BD | ||
| + | |||
| + | 故得證 | ||
| ---- | ---- | ||
| 第35行: | 第47行: | ||
| * 傳統? | * 傳統? | ||
| * 基礎訓練? | * 基礎訓練? | ||
| - | * 訓練什麼? | + | * 訓練什麼? |
| ** 科學思考能力 | ** 科學思考能力 | ||
| ** 科學思考態度 | ** 科學思考態度 | ||
| 第56行: | 第68行: | ||
| ==== 科學家的態度 ==== | ==== 科學家的態度 ==== | ||
| - | * 謙虛: | + | * 謙虛: |
| ** 因為科學中並無永恆不變的真理 | ** 因為科學中並無永恆不變的真理 | ||
| ** 真理或許存在在研究對象背後 | ** 真理或許存在在研究對象背後 | ||
| 第68行: | 第80行: | ||
| ---- | ---- | ||
| - | === <br> === | ||
| === 心實為何考改錯?<br> === | === 心實為何考改錯?<br> === | ||
| 第74行: | 第85行: | ||
| * 給大家體認科學的心理學家如何思考問題 | * 給大家體認科學的心理學家如何思考問題 | ||
| * 在資訊氾濫的時代,學會如何自保 | * 在資訊氾濫的時代,學會如何自保 | ||
| - | * | + | * 身為一個「知識份子」,能夠成為「意見領袖」的技巧養成 |
| * 養成會「說理」、「推理」的習慣與態度 | * 養成會「說理」、「推理」的習慣與態度 | ||
| ==== 如何改錯?1 ==== | ==== 如何改錯?1 ==== | ||
| - | * 第一步 | + | * 第一步 |
| ** 了解問題在何處? | ** 了解問題在何處? | ||
| - | ** | + | ** [http://dbnet.ncl.edu.tw/tsaiani/CONF/CONF-13.HTM 子曰]:「知之為知之,不知為不知,是知也!」 |
| - | * 第二步 | + | * 第二步 |
| ** 那為何是問題? | ** 那為何是問題? | ||
| ** 講道理 | ** 講道理 | ||
| ** 自圓其說 | ** 自圓其說 | ||
| - | + | * 第三步 | |
| - | * 第三步 | + | ** 如果你來做? |
| - | ** | + | |
| ** 知錯能改,善莫大焉 | ** 知錯能改,善莫大焉 | ||
| - | * 第四步 | + | * 第四步 |
| ** 有無想錯? | ** 有無想錯? | ||
| ** 掉入陷阱? | ** 掉入陷阱? | ||
| - | ** | + | ** [http://dbnet.ncl.edu.tw/tsaiani/CONF/CONF-10.HTM 曾子曰]:吾日三省吾身 |
| === 學生狀態 === | === 學生狀態 === | ||
| - | * 漸入佳境 | + | * 漸入佳境 |
| ** 可能開始有一點「手感」 | ** 可能開始有一點「手感」 | ||
| ** 請繼續加油,你們即將得到「科學態度」奧義 | ** 請繼續加油,你們即將得到「科學態度」奧義 | ||
| - | * 快脫離混沌 | + | * 快脫離混沌 |
| ** 似有若無的感覺 | ** 似有若無的感覺 | ||
| ** 其實你們快到了:) | ** 其實你們快到了:) | ||
| - | * 仍然混亂中 | + | * 仍然混亂中 |
| ** 不知如何是好,極端無助 | ** 不知如何是好,極端無助 | ||
| - | ** | + | ** 你們再不來找我,我也無法救你們 |
| ==== 改錯教學 ==== | ==== 改錯教學 ==== | ||
| - | * 修正各位以往可能有問題的思考習慣 | + | * 修正各位以往可能有問題的思考習慣 |
| - | ** | + | ** 《[http://dbnet.ncl.edu.tw/tsaiani/CONF/CONF-35.HTM 論語.述而]》 |
| ** 子曰:「不憤不啟,不悱不發,舉一隅不以三隅反,則不復也。」 | ** 子曰:「不憤不啟,不悱不發,舉一隅不以三隅反,則不復也。」 | ||
當前修訂版本
目錄 |
[編輯] Psychologist, how to
[編輯] 國中為何學數學?
- 買菜有用嗎?
- 國小四則運算即可
- 統計用得到嗎?
- 一點點(如開根號)
- 其實計算上會用計算機就好了
[編輯] 全班60人中至少有兩人的生日是同一天的機率?
解法:
任意二人生日同一日的機率:1/365
所以任意二人生日不同日的機率:1-1/365=364/365
再加一人(即三人)與其他兩人同一生日的機率:2/365
即三人均不同生日的機率:364/365*363/365
以此類推60人均不同生日的機率:364/365*363/365*...306/365*305/365=0.0059(概數)
所以60人中至少有兩人同一天生日的機率為
1-0.0059=0.9941
[編輯] 國中數學是:頭腦體操
- 也是邏輯推理訓練
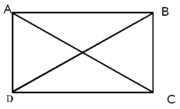
- 試證矩形對角線等長
- 證矩形ABCD之對角線AC=BD
- 即證明三角形ABD與三角形BAC全等(還有其他證法)
因為
線段AD=線段BC
角ADC=角BCD
線段DC=線段CD故三角形ADC全等 三角形BCD(SAS)
推得線段AC=線段BD
故得證
[編輯] 心理學系為何學心實?
- 必修課?
- 傳統?
- 基礎訓練?
- 訓練什麼?
- 科學思考能力
- 科學思考態度
- 科學哲學
[編輯] 科學的可能性
- 科學的極限
- 科學的可靠性
- 以下復習第九講
[編輯] 科學的態度
- 認知:科學是建立在於科學社群脈絡中
- 科學社群:各個相連的人為群體
- 脈絡:不能獨立人類社會活動與歷史
- 目的:想要知道各研究對象的真相
- 真相:可能存在對象的規律性等
[編輯] 科學家的態度
- 謙虛:
- 因為科學中並無永恆不變的真理
- 真理或許存在在研究對象背後
- 科學家想辦法逼近
- 但似乎永遠到不了
[編輯] 拾貝者的畫像
我不知道世人對我如何看待
但我自己卻以為
我是在未知的真理的大海之前
偶遊大海之濱
在海濱上拾一平滑的石塊
或美麗的貝殼
引為歡喜的小孩子
[編輯] 心實為何考改錯?
- 給大家體認科學的心理學家如何思考問題
- 在資訊氾濫的時代,學會如何自保
- 身為一個「知識份子」,能夠成為「意見領袖」的技巧養成
- 養成會「說理」、「推理」的習慣與態度
[編輯] 如何改錯?1
- 第一步
- 了解問題在何處?
- 子曰:「知之為知之,不知為不知,是知也!」
- 第二步
- 那為何是問題?
- 講道理
- 自圓其說
- 第三步
- 如果你來做?
- 知錯能改,善莫大焉
- 第四步
- 有無想錯?
- 掉入陷阱?
- 曾子曰:吾日三省吾身
[編輯] 學生狀態
- 漸入佳境
- 可能開始有一點「手感」
- 請繼續加油,你們即將得到「科學態度」奧義
- 快脫離混沌
- 似有若無的感覺
- 其實你們快到了:)
- 仍然混亂中
- 不知如何是好,極端無助
- 你們再不來找我,我也無法救你們
[編輯] 改錯教學
- 修正各位以往可能有問題的思考習慣
- 《論語.述而》
- 子曰:「不憤不啟,不悱不發,舉一隅不以三隅反,則不復也。」