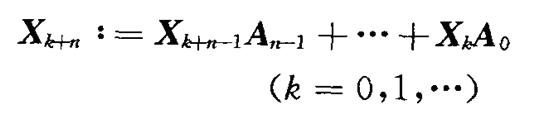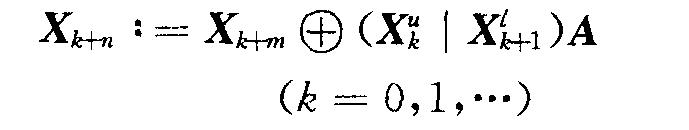亂數產生器-Mersenne Twister Random Number Generator
出自KMU Wiki
(修訂版本間差異)
| 在2008年5月2日 (五) 01:30所做的修訂版本 (編輯) Mo (對話 | 貢獻) (新頁面: Mersenne Twister(簡稱MT )在1998年由Makoto和Takuji提出的,是多重遞迴矩陣方法(MRMM)中的一種,MRMM是在F2域上由線性遞推式 Image:MRMM.JPG 產生隨...) ←上一個 |
在2008年5月2日 (五) 01:57所做的修訂版本 (編輯) (撤銷) Mo (對話 | 貢獻) 下一個→ |
||
| 第6行: | 第6行: | ||
| [[Image:MRMM.JPG]] | [[Image:MRMM.JPG]] | ||
| + | <br>產生隨機向量序列。Xk是列向量,Ai是Wx W矩陣。 | ||
| - | + | 而MT演算法產生一個字(word)向量序列,看作是[0,2的w次方-1]間的均勻隨機整數。除以2的w次方-1,認為每個字向量為[0,1]的一個實數。 算法如下: | |
| + | [[Image:MRMM-1.JPG]] | ||
| - | x W矩陣。 | ||
| - | + | n=遞推式的維數,0 | |
| + | |||
| + | |||
| + | <=r(隱藏於Xuk的定義中)<=w-1,1<=m<=n 。給出X0,X1,...Xn-1作為初始點,那麼Xn由上面的式子再k=0時產生,令k=1,2,...,亂數產生器逐步產生Xn+1,Xn+2,...,在式子的右邊,Xuk意味著Xk前w-r位,因此如果X=(Xw-1,Xw-2,...,X0),那麼由定義,Xu是w-r維向量(Xw-1,...,Xr),Xt是r維向量(Xr-1,...,X0)。因此(Xuk|X上標t下標k+1)恰好是一個並列,即Xk前w-r位和Xk+1的後r位按順序並列再一起得到的一個向量。矩陣A乘在這個向量的右邊。(XOR舉例:1 XOR 1=0 XOR 0,1 XOR 0=0 XOR 1=1) | ||
在2008年5月2日 (五) 01:57所做的修訂版本
Mersenne Twister(簡稱MT
)在1998年由Makoto和Takuji提出的,是多重遞迴矩陣方法(MRMM)中的一種,MRMM是在F2域上由線性遞推式
產生隨機向量序列。Xk是列向量,Ai是Wx W矩陣。
而MT演算法產生一個字(word)向量序列,看作是[0,2的w次方-1]間的均勻隨機整數。除以2的w次方-1,認為每個字向量為[0,1]的一個實數。 算法如下:
n=遞推式的維數,0
<=r(隱藏於Xuk的定義中)<=w-1,1<=m<=n 。給出X0,X1,...Xn-1作為初始點,那麼Xn由上面的式子再k=0時產生,令k=1,2,...,亂數產生器逐步產生Xn+1,Xn+2,...,在式子的右邊,Xuk意味著Xk前w-r位,因此如果X=(Xw-1,Xw-2,...,X0),那麼由定義,Xu是w-r維向量(Xw-1,...,Xr),Xt是r維向量(Xr-1,...,X0)。因此(Xuk|X上標t下標k+1)恰好是一個並列,即Xk前w-r位和Xk+1的後r位按順序並列再一起得到的一個向量。矩陣A乘在這個向量的右邊。(XOR舉例:1 XOR 1=0 XOR 0,1 XOR 0=0 XOR 1=1)