ANSI X9.17 虛擬亂數產生器
出自KMU Wiki
(修訂版本間差異)
| 在2008年5月1日 (四) 00:49所做的修訂版本 (編輯) U9314017 (對話 | 貢獻) (新頁面: = '''ANSI X9.17 虛擬亂數產生器''' = * '''ANSI X9.17 PRNG (Pseudo Random Number Generator)''' <br> <dl><dd>依據ANSI 9.17標準</dd><dd>使用3重DES演算...) ←上一個 |
當前修訂版本 (2008年5月1日 (四) 22:11) (編輯) (撤銷) U9314017 (對話 | 貢獻) 小 |
||
| (3個中途的修訂版本沒有顯示。) | |||
| 第1行: | 第1行: | ||
| = '''ANSI X9.17 虛擬亂數產生器''' = | = '''ANSI X9.17 虛擬亂數產生器''' = | ||
| - | * '''ANSI X9.17 PRNG ([[ | + | * '''ANSI X9.17 PRNG ([[Pseudo Random Number Generator]])''' |
| + | |||
| + | 依據[[ANSI917|ANSI 9.17]]標準 | ||
| + | |||
| + | 使用3重DES演算法([[3DES|Triple-DES]]) | ||
| + | |||
| + | 參數 | ||
| - | <br> | ||
| - | <dl><dd>依據[[ANSI917|ANSI 9.17]]標準</dd><dd>使用3重DES演算法([[3DES|Triple-DES]])</dd><dd>參數 | ||
| # 第 i 個回合(generation stage) | # 第 i 個回合(generation stage) | ||
| # DT<sub>i</sub>: 當時日期與時間(Date,Time以64 bits表示) | # DT<sub>i</sub>: 當時日期與時間(Date,Time以64 bits表示) | ||
| 第11行: | 第15行: | ||
| # K<sub>1</sub>, K<sub>2</sub>:Triple DES keys(每個模組使用兩把相同的56位元鑰匙共112 bits (56*2)) | # K<sub>1</sub>, K<sub>2</sub>:Triple DES keys(每個模組使用兩把相同的56位元鑰匙共112 bits (56*2)) | ||
| # 輸出:64位元虛擬亂數值(R<sub>i</sub>)與64位元下回合之起始值(V<sub>i+1</sub>) | # 輸出:64位元虛擬亂數值(R<sub>i</sub>)與64位元下回合之起始值(V<sub>i+1</sub>) | ||
| - | < | + | |
| - | 演算法輸出: | + | <br>演算法輸出: |
| R<sub>i</sub>= 3DES<sub>K1,K2</sub><sub></sub>[ V<sub>i</sub>⊕ 3DES<sub>K1,K2</sub>[ DT<sub>i</sub>] ] | R<sub>i</sub>= 3DES<sub>K1,K2</sub><sub></sub>[ V<sub>i</sub>⊕ 3DES<sub>K1,K2</sub>[ DT<sub>i</sub>] ] | ||
| 第18行: | 第22行: | ||
| V<sub>i+1</sub>= 3DES<sub>K1,K2</sub>[ R<sub>i</sub>⊕ 3DES<sub>K1,K2</sub><sub></sub>[ DT<sub>i</sub> ] ] | V<sub>i+1</sub>= 3DES<sub>K1,K2</sub>[ R<sub>i</sub>⊕ 3DES<sub>K1,K2</sub><sub></sub>[ DT<sub>i</sub> ] ] | ||
| - | <br> | + | <br>[[Image:ANSI.PNG]] |
當前修訂版本
[編輯] ANSI X9.17 虛擬亂數產生器
- ANSI X9.17 PRNG (Pseudo Random Number Generator)
依據ANSI 9.17標準
使用3重DES演算法(Triple-DES)
參數
- 第 i 個回合(generation stage)
- DTi: 當時日期與時間(Date,Time以64 bits表示)
- Vi: 起始值(seed value)
- Ri: 產生的Pseudo-random number
- K1, K2:Triple DES keys(每個模組使用兩把相同的56位元鑰匙共112 bits (56*2))
- 輸出:64位元虛擬亂數值(Ri)與64位元下回合之起始值(Vi+1)
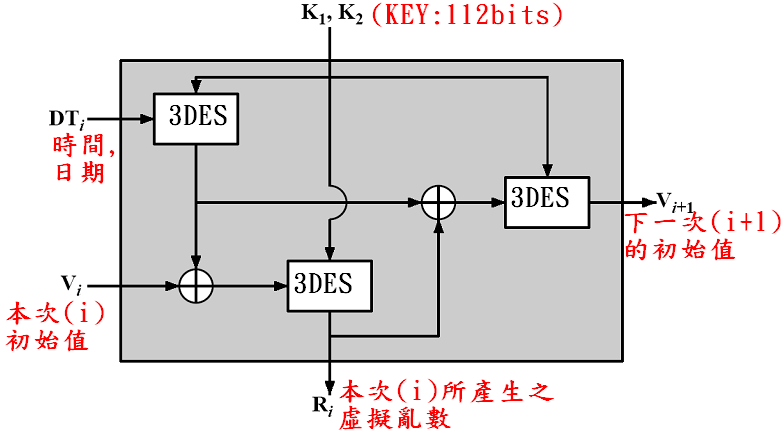
演算法輸出:
Ri= 3DESK1,K2[ Vi⊕ 3DESK1,K2[ DTi] ]
Vi+1= 3DESK1,K2[ Ri⊕ 3DESK1,K2[ DTi ] ]